这是一个创建于 2400 天前的主题,其中的信息可能已经有所发展或是发生改变。

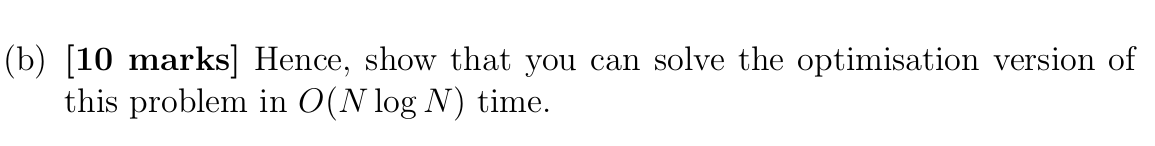 第一小题目前的想法是用 i,j 分别从头和尾找比 T 大的元素,如果没找到,直接返回 false。如果找到了,但是 j - i <= k, 返回 L == 1 如果 j - i > k,L -= 2,i 和 j 分别前进 k+1,继续找。最后判断 L 是不是等于 0。但是不知道这个思路是否正确。
第二小题就卡住了,没有找到可行的办法
第一小题目前的想法是用 i,j 分别从头和尾找比 T 大的元素,如果没找到,直接返回 false。如果找到了,但是 j - i <= k, 返回 L == 1 如果 j - i > k,L -= 2,i 和 j 分别前进 k+1,继续找。最后判断 L 是不是等于 0。但是不知道这个思路是否正确。
第二小题就卡住了,没有找到可行的办法
1
xml123 2018-04-11 22:17:18 +08:00
先翻译一下题目(以确定我没有理解错题目):
给定一个长度为 N 的数列 H,从中取出 L 个元素,要求取出的每个元素在数列中的距离要大于 K,目标是使得取出元素的最小值尽可能大。 (1)用 O(N)的时间使最小值不小于 T (或不存在满足条件的取法); (2)用 O(N log N)的时间找出最优解。 第一问应该只要从左开始不断取出不小于 T 且距离上一个取出的元素大于 K 的数就行了。 第二问我目前只能想出一个最笨的方法,先用 O(N log N)的时间给数列排序,然后不断调用第一问的方法,二分法确定最小值可以是多少,相当于二分法找有序数列里的一个数,用的次数的 log N,这样花的时间也是 O(N log N)。 |
2
letianqiu OP @xml123 和我后来的想法一样。但是第一问不确定,感觉上这样不会漏解。我改进过的想法是遍历数组,如果当前元素小于 T,i++, 否则 L--, i 前进 k+1。循环的条件是 L>0。最后判断 L 是否等于 0。第二问我后来也只想出排序之后类似二分查找调用第一问的方法,如果 ok,记录当前元素,继续后半部分,否则就在前半部分测试
|
3
RecursiveG 2018-04-12 03:19:28 +08:00 via Android
a 小问贪心法,b 小问二分答案法。具体方法就和 @xml123 说的一样。
|